Площа кола: формула. Чому дорівнює площа кола, описаного і вписаного в квадрат, і прямокутний рівнобедрений трикутник, прямокутну, равнобедренную трапецію?

Як знайти площу круга? Спочатку знайдіть радіус. Вчіться вирішувати прості і складні завдання.
Зміст
- Площа кола: формула через радіус, діаметр, довжину окружності, приклади розв'язання задач
- Площу круга, вписаного в квадрат: формула, приклади розв'язання задач
- Площу круга, описаного близько квадрата: формула, приклади розв'язання задач
- Площу круга, вписаного в прямокутний і рівнобедрений трикутник: формула, приклади розв'язання задач
- Площу круга, описаного близько прямокутного і рівнобедреного трикутника: формула, приклади розв'язання задач
- Площу круга, вписаного в прямокутний і равнобедренную трапецію: формула, приклади розв'язання задач
- Площу круга, описаного близько прямокутної і равнобедренной трапеції: формула, приклади розв'язання задач
- Відео: Математика | Обчислення площ круга і його частин
Коло — це замкнута крива. Будь-яка точка на лінії окружності буде знаходитися на однаковій відстані від центральної точки. Коло — це плоска фігура, тому вирішувати завдання із знаходженням площі просто. У цій статті ми розглянемо, як знайти площу круга, вписаного в трикутник, трапеція, квадрат, і описаного біля цих фігур.
Площа кола: формула через радіус, діаметр, довжину окружності, приклади розв'язання задач
Щоб знайти площу фігури, потрібно знати, що таке радіус, діаметр і число π.
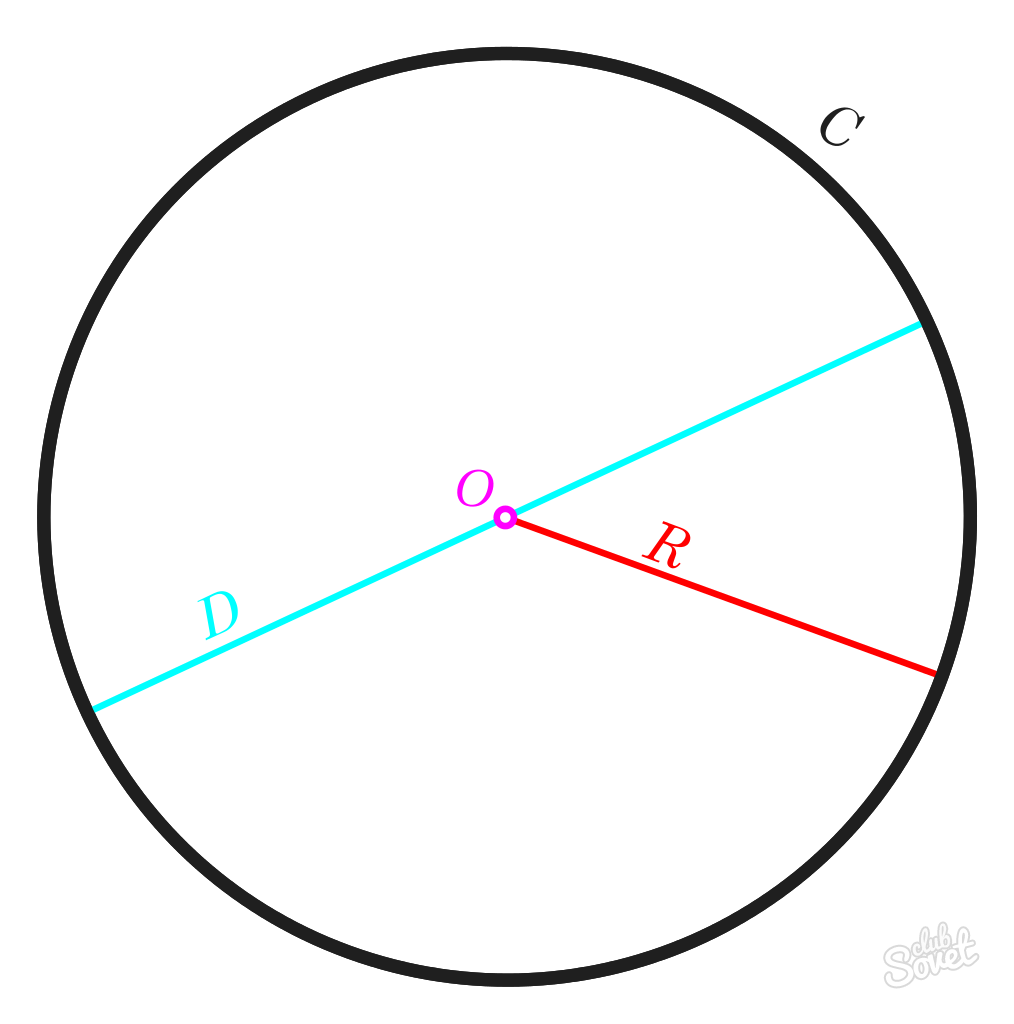
Радіус R — це відстань, обмежене центром окружності. Довжини всіх R-радіусів одній окружності будуть рівними.
Діаметр D — це лінія між двома будь-якими точками кола, що проходить через центральну точку. Довжина цього відрізка дорівнює довжині R-радіуса, помноженої на 2.
Число π — це незмінна величина, яка дорівнює 3,1415926. В математиці зазвичай це число округлюється до 3,14.
Формула знаходження площі круга через радіус:
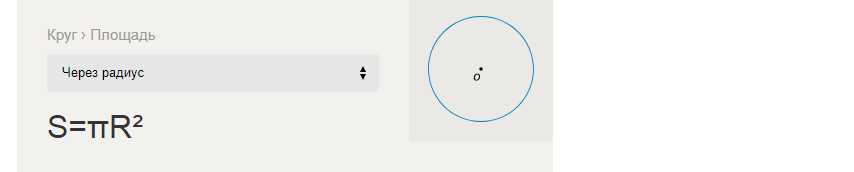
Приклади рішення завдань по знаходженню S-площі кола через R-радіус:
----------------------------------------
Завдання: Знайдіть площу кола, якщо його радіус дорівнює 7 див.
Рішення: S=πR2, S=3,14*72, S=3,14*49=153,86 см2.
Відповідь: Площа кола дорівнює 153,86 см2.
Формула знаходження S-площі кола через D-діаметр:

Приклади рішення завдань по знаходженню S, якщо відомий D:
-----------------------------------------
Завдання: Знайдіть S кола, якщо його D дорівнює 10 див.
Рішення: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 см2.
Відповідь: Площа плоскої круглої фігури дорівнює 78,5 см2.
Знаходження S кола, якщо відома довжина кола:
Спочатку знаходимо, чому дорівнює радіус. Довжина окружності розраховується за формулою: L=2πR, відповідно радіус R буде дорівнює L/2π. Тепер знаходимо площу кола за формулою через R.
Розглянемо рішення на прикладі задачі:
----------------------------------------
Завдання: Знайдіть площу круга, якщо відома довжина кола L — 12 див.
Рішення: Спочатку знаходимо радіус: R=L/2π=12/2*3,14=12/6,28=1,91.
Тепер знаходимо площу через радіус: S=πR2=3,14*1,912=3,14*3,65=11,46 см2.
Відповідь: Площа круга дорівнює 11,46 см2.
Площу круга, вписаного в квадрат: формула, приклади розв'язання задач
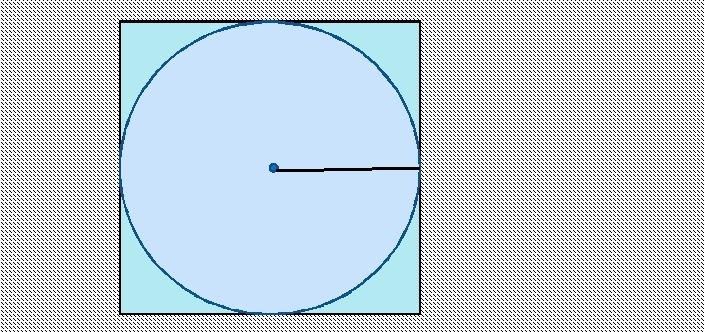
Знайти площу круга, вписаного в квадрат просто. Сторона квадрата — це діаметр кола. Щоб знайти радіус, потрібно бік розділити на 2.
Формула знаходження площі кола, вписаного в квадрат:

Приклади розв'язання задач на знаходження площі кола, вписаного в квадрат:
---------------------------------------
Завдання №1: Відома сторона квадратної фігури, яка дорівнює 6 сантиметрів. Знайдіть S-площа вписаного кола.
Рішення: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 см2.
Відповідь: Площа плоскої круглої фігури дорівнює 28,26 см2.
----------------------------------------
Завдання №2: Знайдіть S кола, вписаного в квадратну фігуру і його радіус, якщо одна сторона дорівнює a=4 див.
Вирішуйте так: Спочатку знайдемо R=a/2=4/2=2 див.
Тепер знайдемо площу кола S=3,14*22=3,14*4=12,56 см2.
Відповідь: Площа плоскої круглої фігури дорівнює 12,56 см2.
Площу круга, описаного близько квадрата: формула, приклади розв'язання задач
Трохи складніше знаходити площу круглої фігури, описаної близько квадрата. Але, знаючи формулу, можна швидко підрахувати дане значення.
Формула знаходження S кола, описаного близько квадратної фігури:

Приклади розв'язання завдань на знаходження площі кола, описаної близько квадратної фігури:
Завдання

Площу круга, вписаного в прямокутний і рівнобедрений трикутник: формула, приклади розв'язання задач
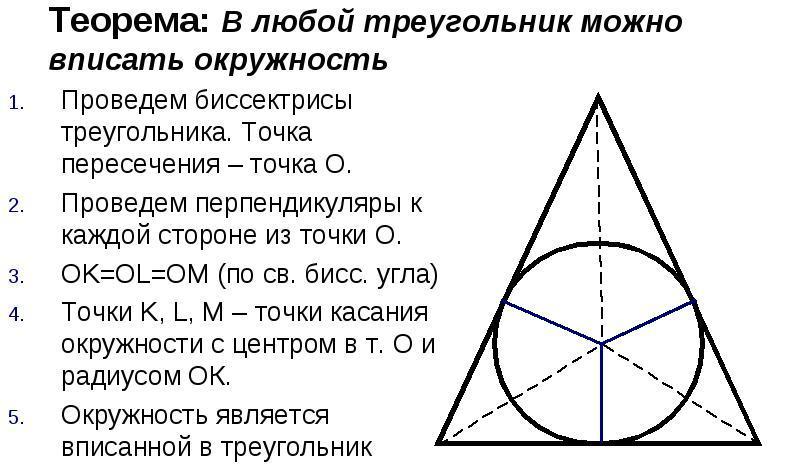
Окружність, яка вписана в трикутну фігуру — круг, який стосується всіх трьох сторін трикутника. У будь-яку трикутну фігуру можна вписати коло, але тільки один. Центром кола буде точка перетину бісектрис кутів трикутника.
Формула знаходження площі кола, вписаного в рівнобедрений трикутник:
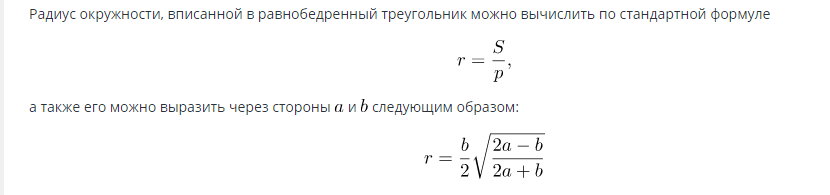
Коли буде відомий радіус, площа можна обчислити за формулою: S=πR2.
Формула знаходження площі кола, вписаного в прямокутний трикутник:
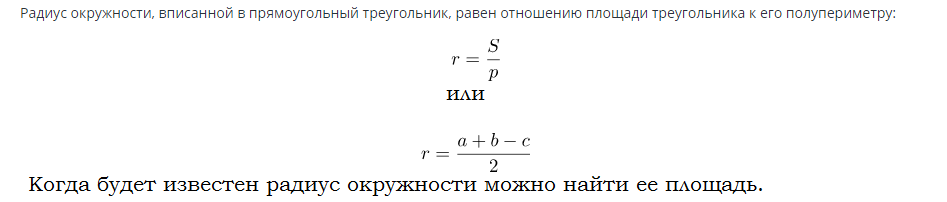
Приклади рішення завдань:
Завдання №1

Якщо в цій задачі треба знайти ще й площа кола з радіусом 4 см, то зробити це можна за формулою: S=πR2
Завдання №2
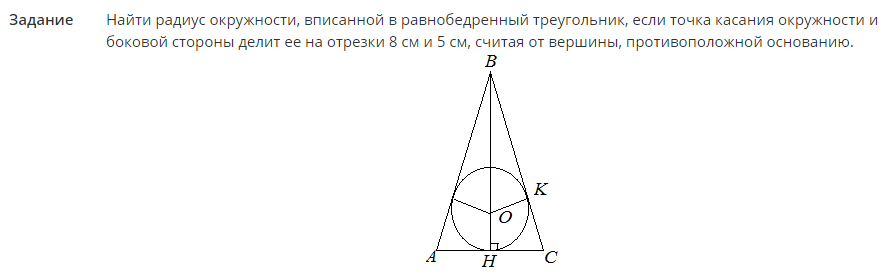
Рішення:

Тепер, коли відомий радіус, можна знайти площу круга через радіус. Формулу дивіться вище по тексту.
Завдання №3

Площу круга, описаного близько прямокутного і рівнобедреного трикутника: формула, приклади розв'язання задач
Всі формули щодо знаходження площі кола зводяться до того, що спочатку потрібно знайти його радіус. Коли відомий радіус, то знайти площу просто, як було описано вище.
Площу круга, описаного близько прямокутного і рівнобедреного трикутника знаходиться за такою формулою:
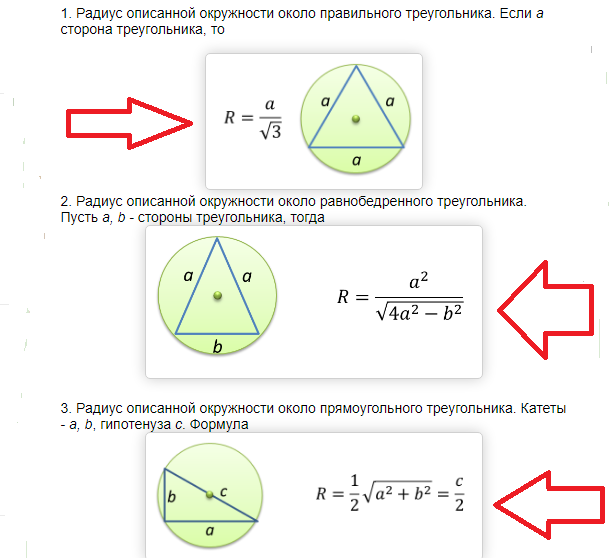
Приклади розв'язання задач:

Ось ще приклад розв'язання задачі з використанням формули Герона.
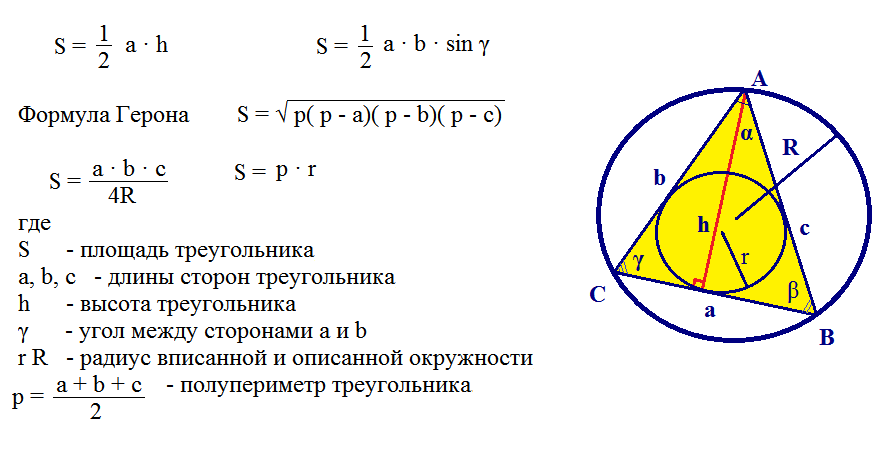
Вирішувати подібні завдання складно, але їх можна здолати, якщо знати всі формули. Такі завдання школярі вирішують у 9 класі.
Площу круга, вписаного в прямокутний і равнобедренную трапецію: формула, приклади розв'язання задач
Наприклад, в равнобедренную трапецію вписано коло, що в точці дотику ділить одну сторону на відрізки m і n.
Для вирішення цього завдання потрібно використовувати такі формули:

Знаходження площі кола, вписаного в прямокутну трапецію, проводиться за наступною формулою:
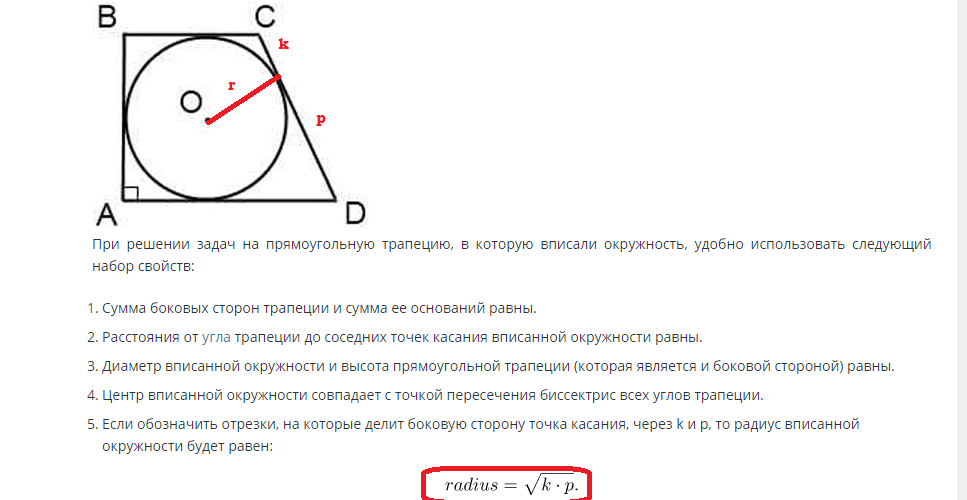
Якщо відома бічна сторона, то можна знайти радіус через це значення. Висота бічної сторони трапеції дорівнює діаметру кола, а радіус — це половина діаметра. Відповідно, радіус дорівнює R=d/2.
Приклади розв'язання задач:

Площу круга, описаного близько прямокутної і равнобедренной трапеції: формула, приклади розв'язання задач
Трапецію можна вписати в коло, коли сума протилежних кутів дорівнює 180°. Тому можна вписати тільки равнобокую трапецію. Радіус для обчислення площу круга, описаного близько прямокутної або равнобедренной трапеції, розраховується за такими формулами:

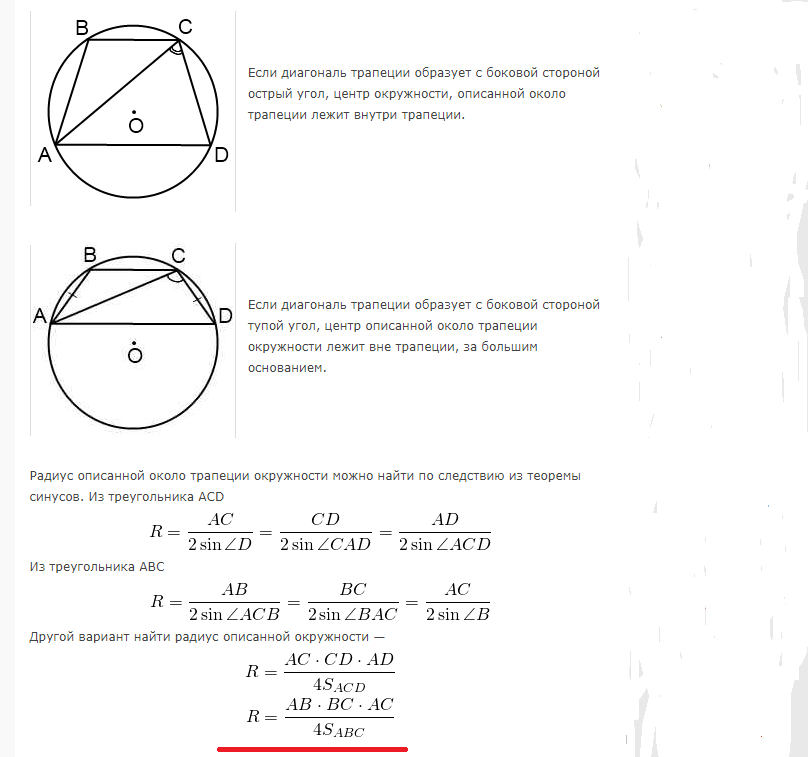
Приклади розв'язання задач:
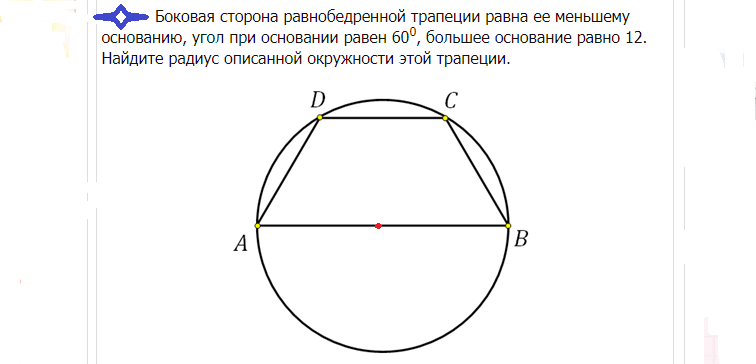
Рішення: Велика основа в цьому випадку проходить через центр, так як у коло вписано равнобедренная трапеція. Центр ділить це підстава рівно навпіл. Якщо основа АВ дорівнює 12, тоді радіус R можна знайти так: R=12/2=6.
Відповідь: Радіус дорівнює 6.
В геометрії важливо знати формули. Але все їх неможливо запам'ятати, тому навіть на багатьох іспитах дозволяється користуватися спеціальним формуляром. Проте важливо вміти знаходити правильну формулу для рішення тієї або іншої задачі. Тренуйтеся в рішенні різних задач на знаходження радіусу і площі кола, щоб уміти правильно підставляти формули і отримувати точні відповіді.