Рівносторонній трикутник: всі правила
У цій статті описані всі властивості, правила і визначення рівностороннього трикутника.
Математика — улюблений предмет багатьох школярів, особливо тих, у яких виходить вирішувати завдання. Геометрія — це також цікава наука, але не всі діти можуть зрозуміти новий матеріал на уроці. Тому їм доводиться допрацьовувати і доучувати будинку. Давайте повторимо правила рівностороннього трикутника. Читайте нижче.
Всі правила рівностороннього трикутника: властивості
У самому слові «рівносторонній» ховається визначення цієї фігури.
Визначення рівностороннього трикутника: Це трикутник, у якого всі сторони рівні один одному.
З-за того, що рівносторонній трикутник – це в деякому роді рівнобедрений трикутник, у нього з'являються ознаки останнього. Наприклад, в цих трикутниках бісектриса кута є ще медіаною і висотою.
Згадаймо: Бісектриса — промінь, який ділив кут навпіл, медіана – промінь, випущений з вершини, ділив противолежащую сторону навпіл, а висота — це перпендикуляр, що виходить з вершини.
Другою ознакою рівностороннього трикутника є те, що усі його кути рівні між собою і кожна з них має градусну міру в 60 градусів. Висновок про це можна зробити з загального правила про суму кутів трикутника дорівнює 180 градусам. Отже, 180:3=60.
Наступна властивість: центром рівностороннього трикутника, а також вписаною в нього й описаного біля нього кола є точка перетину всіх його медіан (бісектрис).

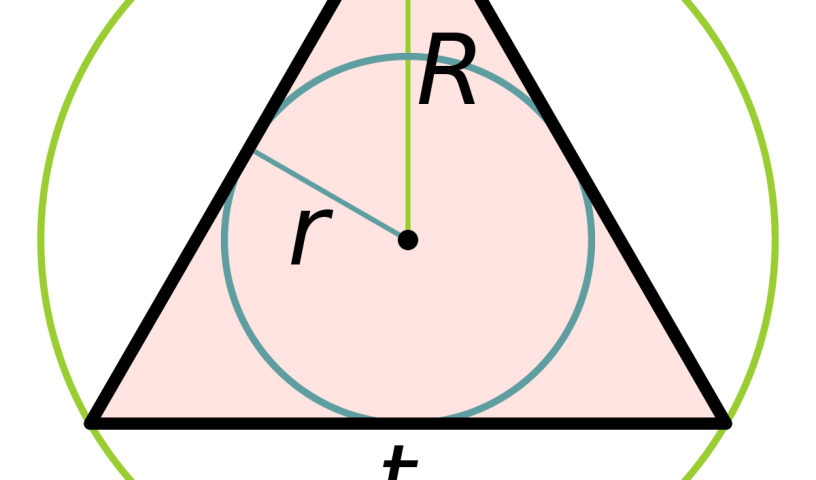
Четверта властивість: радіус описаної близько рівностороннього трикутника кола перевищує в два рази радіус вписаного кола в цю фігуру. Переконатися в цьому можна, подивившись на креслення. ОС є радіусом описаної близько трикутника кола, а ОВ1 — радіусом вписаного. Точка О — місце перетину медіан, значить, розділяє її як 2:1. З цього робимо висновок, що ОС = 2ОВ1.
П'ятим властивістю є те, що в цій геометричній фігурі легко порахувати складові елементи, якщо умови вказана довжина однієї сторони. При цьому найчастіше використовується теорема Піфагора.
Шосте властивість: площу такого трикутника обчислюється за формулою S=(а^2*3) /4.
Сьома властивість: радіуси окружності, описаної близько трикутника, і кола, вписаного в трикутник, відповідно дорівнюють
R = (a3) /3 і r = (a3) /6.
Розглянемо приклади завдань:
Приклад 1:
Завдання: Радіус кола, вписаного в рівносторонній трикутник дорівнює 7 див. Знайдіть висоту трикутника.
Рішення:
- Радіус вписаного кола пов'язаний з останньою формулою, отже, OM = (BC3) /6.
- BC = (6 * OM) /3 = (6*7) /3 = 143.
- AM = (BC3) /2; AM = (143*3) /2 = 21.
- Відповідь: 21 див.
Цю задачу можна вирішити по-іншому:
- Виходячи з четвертого властивості, можна зробити висновок, що ОМ = 1/2 АМ.
- Отже, якщо ОМ дорівнює 7, то АТ дорівнює 14, а АМ дорівнює 21.
Приклад 2:
Завдання: Радіус описаної близько трикутника кола дорівнює 8. Знайдіть висоту трикутника.
Рішення:
- Нехай АВС – рівносторонній трикутник.
- Як і в попередньому прикладі, можна йти двома шляхами: більш простим – АТ = 8 = ОМ =4. Тоді АМ = 12.
- І більш довгим – щоб знайти АМ через формулу. АМ = (АС3) /2 = (83*3) /2 = 12.
- Відповідь: 12.
Як бачите, знаючи властивості й означення рівностороннього трикутника, ви зможете вирішити будь-яку задачу з геометрії по цій темі.